- Variété linéaire affine
-
● Variété linéaire affine sous-ensemble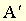 d'un espace affine A, tel que tous les barycentres d'une famille finie quelconque de points Mi de
d'un espace affine A, tel que tous les barycentres d'une famille finie quelconque de points Mi de 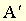 appartiennent à
appartiennent à 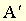 .
.
Encyclopédie Universelle. 2012.
● Variété linéaire affine sous-ensemble
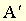 d'un espace affine A, tel que tous les barycentres d'une famille finie quelconque de points Mi de
d'un espace affine A, tel que tous les barycentres d'une famille finie quelconque de points Mi de 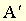 appartiennent à
appartiennent à 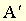 .
.Encyclopédie Universelle. 2012.
affine — [ afin ] adj. • XXe; fém. de affin 1 ♦ Biol. Formes affines, présentant des ressemblances ne traduisant pas toujours des liens de parenté. Les sélaginelles sont affines aux lycopodes. 2 ♦ Math. Transformation affine : transformation dans le plan… … Encyclopédie Universelle
Variete affine — Variété affine Soit A un espace affine rattaché à un espace vectoriel E. On dit qu une partie non vide A de A est une variété linéaire affine ou un sous espace affine, si pour tout point M de A , l ensemble E des vecteurs MN de E, où N appartient … Wikipédia en Français
linéaire — [ lineɛr ] adj. et n. m. • XVe; lat. linearis, de linea → ligne 1 ♦ Qui a rapport aux lignes, se traduit par des lignes. Mesure linéaire : mesure de longueur. Dessin linéaire, où le trait seul est utilisé (cf. Au trait). Perspective linéaire… … Encyclopédie Universelle
Variété affine — Ne doit pas être confondu avec les variétés algébriques affines en géométrie algébrique En géométrie affine, un sous espace affine (ou variété linéaire affine) d un espace affine A est une partie de A héritant d une structure d espace… … Wikipédia en Français
Variete algebrique — Variété algébrique Pour les articles homonymes, voir variété. Une variété algébrique est, de manière informelle, l ensemble des racines communes d un ensemble de polynômes en plusieurs indéterminées. La géométrie algébrique est la théorie qui… … Wikipédia en Français
Espace affine — En géométrie, un espace affine est un espace qui généralise la notion d espace vectoriel. Dans un espace affine on peut parler d alignement, de parallélisme, de rapport de proportionnalité. Sous la forme qui utilise des rapports de mesures… … Wikipédia en Français
Connexion affine — Une connexion affine sur la sphère fait rouler le plan affine tangent d un point à un autre. Dans ce déplacement, le point de contact trace une courbe du plan : le développement. En mathématiques, et plus précisément en géométrie… … Wikipédia en Français
Théorème fondamental de la géométrie affine — En géométrie, le théorème fondamental de la géométrie affine est un théorème qui caractérise algébriquement les bijections entre espaces affines qui présevent l alignement des points. Avec quelques hypothèses, il dit qu une bijection entre deux… … Wikipédia en Français
Barycentre (Géométrie Affine) — Pour les articles homonymes, voir Barycentre. En géométrie affine, le barycentre de plusieurs points affectés de coefficients est un point annulant une certaine égalité vectorielle. Le calcul de barycentre est l outil fondamental de la géométrie… … Wikipédia en Français
Barycentre (géométrie affine) — Pour les articles homonymes, voir Barycentre. En géométrie affine, le barycentre de plusieurs points affectés de coefficients est un point annulant une certaine égalité vectorielle. Le calcul de barycentre est l outil fondamental de la géométrie… … Wikipédia en Français